The Planck-scale physics story begins long ago. In 1901 German physicist Max Planck publishes an explanation for strange properties of radiant heat. He says its energy is quantized. In other words, it radiates in distinct little bits. He sees this as a mathematical convenience and doesn’t really believe it.

His math requires a constant he calls h, short for Hilfsgrösse, or big help. He does not foresee it will soon be called Planck’s constant and kick off quantum theory. It’s tiny: Planck calculates it to be 6.55×10-34 joule second. (Today it’s measured to be 6.62607004×10-34.)

It is now the most fundamental number in the universe; Planck says it leads in turn to fundamental units.

Time and length and volume have familiar units—like days, meters, gallons—patched together from arbitrary sources like Earth’s rotation, the distance from pole to pole and even an old jug of wine. By contrast, Planck units are properties of the universe itself.

Like h, Planck units are tiny. The Planck length is almost a billion-billion-billion-billion times smaller than a meter. The Planck volume is about 4×10-102 liters. You could pack some seven hundred billion-billion-billion-billion-billion-billion Planck volumes into a proton, whose volume is a quadrillion times less than that of an atom.

String theories say there is nothing smaller than the Planck volume. Like Planck, string theorists tend not to take this literally. They should: It now looks like the universe is made of these tiny volumes.

In 1854 Bernhard Riemann showed how to do geometry in curved spaces of various dimensions. He said one must make an assumption about the kind of space: Is it smooth and continuous at all scales or is it granular and made of little bits or flecks at small scales? He said one should choose the kind that represents reality.

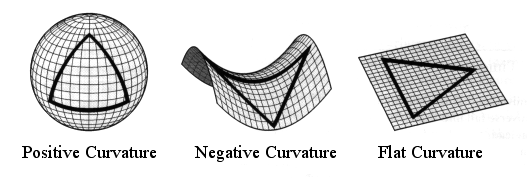In 1915 Albert Einstein used Riemann’s geometry to build his theory of general relativity. He chose to assume space is smooth. By 1956 he had come to think this was a big mistake. For a thousand years science has sought the answer to a simple question: What is the world made of? In this long search, smooth space was a costly detour.

For fifty years physics has built its Standard Model based on smooth space. It says the world is made of 92 kinds of atoms; and they in turn are made of 25 kinds of fundamental subatomic particles. These particles have various electric charges: 0, ±e, or ±e/3, where e is the charge on the electron.

Of course that leads to the next question: What are they made of?

The answer takes us to a world far smaller than subatomic—the world Planck foreshadowed, though he didn’t know it. This is where the Planck-scale rubber hits the physics road.

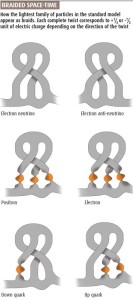
In 2005 Australian physicist Sundance Bilson-Thompson revealed how all 92 atoms and all 25 subatomic particles can be built using just one kind of thing—a Planck-scale twist that is an electric charge of e/6.

That is, the supposedly fundamental subatomic particles are not fundamental. They are composite and so are their electric charges. And they are made of braided twists of space.

Is Bilson-Thompson’s Planck-scale twist the indivisible a-tom ancient Greeks imagined? He does not claim so. But string theory agrees with Planck that no smaller scale exists. And matter can hardly have fewer ingredients than just one.

It’s been a long road from the very large to the very small. It began in the night skies. It leads to the latest and perhaps final frontier for physics—the study of the world that really is.

Image credits:

http://abyss.uoregon.edu/~js/cosmo/lectures/lec15.html

https://www.newscientist.com/data/images/archive/2564/25645802.jpg