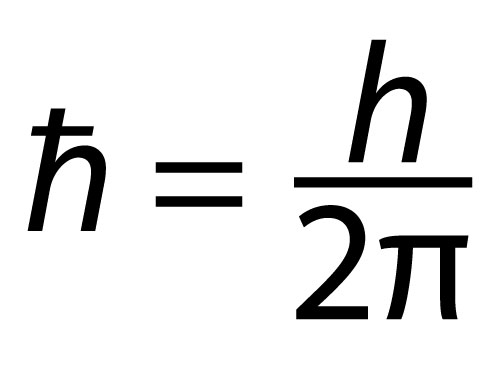
Some numbers in the universe feel far too small. Of course a number can be anything; its size cannot be wrong. It is a gut-feel thing. For example Penrose finds the mass of the electron ‘absurdly tiny’. It’s not the only number feel-for-physics finds too small.

The most basic numbers bear the name of Planck.

In the 1800s a philosopher, George Stoney, worked on numbers. He disliked arbitrary units, like the length of someone’s foot that holds sway to this day. He thought there should be units that are natural. He proposed basic units for time, mass and size. They turned out to be tiny. Then Planck proposed similar ideas. Planck’s constant is a fundamental number. It shows up in Heisenberg’s Uncertainty Principle. It’s very small. Then there’s a Planck time. Compared to times that can be measured it is very small. And there’s the Planck size of which Penrose says, ‘This distance is considered to be of profound relevance in quantum gravity theory.’ The width of a hydrogen atom is about a billionth of that of a baseball. The proton at its center is about a hundred thousand times smaller again. Ridiculously small. The Planck size is some 100,000,000,000,000,000,000 times smaller than the proton. Why is this size so small compared to things that are ridiculously small? It’s like physics has a ruler that’s too tiny. One way to view the Problem of Small Numbers is: If the standard ruler is much smaller than an atom what is going on down there at sizes where it’s useful?