General relativity says spacetime is curved. It is similar to saying that the surface of the earth is curved. The curve’s so slight the curvature is easy to forget. It has local bumps and wrinkles. But overall the 2-D surface of the earth is curved more or less like a sphere.

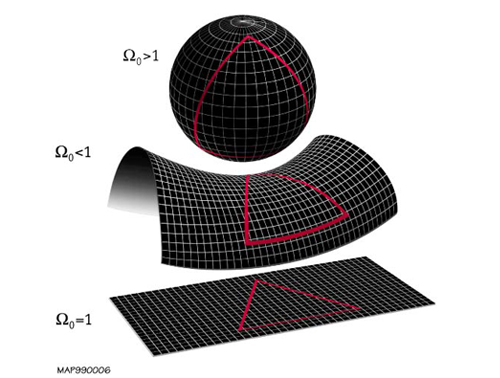
Spacetime could be curved like a sphere too. A sphere curves the same way fore-and-aft and side-to-side. A curvature that curves the same way both ways is called positive. A bigger sphere has smaller curvature.

There’s another kind of surface curve. It’s like a saddle. It curves up fore-and-aft and down side-to-side or vice versa. This curvature’s called negative. In between the two kinds there is zero curvature. This is called flat. The question is then: What’s the universe’s curvature? Is it positive or negative; or is it flat?

Spacetime being 4-D means the universe is curved in four dimensions. Its curvature depends upon the average density of matter in the universe. If the density is high enough, the curvature is positive. If it’s low enough, the curvature is negative. And if it is exactly a certain density, the universe is flat. Its curvature determines what it does. If its curvature is even slightly positive, gravity will bring the matter back together at some future date in a Big Crunch. But if its curvature is even slightly negative it will expand forever, slowing down but never coming to a stop.

Measurements show that the universe is flat to a degree that seems to make no sense. It’s like a pencil balanced on its point for 13 billion years without a wobble. Why is the universe so close to flat? Something must have made it flat way back. But what?