Time matters to us all. We are defined by time. Mostly we don’t think about it. But it’s easier to think about than you might expect.

Time became important in the 15^th century. It came to be synonymous with clocks. Accurate chronometers would help sailors figure where they were at sea. Many made bold voyages—or lost their lives—before 1765 when John Harrison, an English clockmaker, built an accurate chronometer (and won a quarter-billion-dollar prize with it).

Today precise time is even more important. It is entrenched deep in our economy. For example, telling time high and low, here and there, is what makes GPS work, leading to hundreds of applications that support millions of jobs. Time, one might think cheerfully, has come of age.

Sad to say, the fact is we are losing time, losing it as a concept that we thought we understood. Many physicists (our prime timekeepers) say maybe there is no such thing. Time, they say—the t in their equations—is an illusion. Just as we find time within our grasp—or so we thought—our grasp of what time is seems to be slipping. What went wrong? And can we fix it?

What went wrong began in the 1600s when Italian astronomer Galileo Galilei proposed the principle of relativity. It seemed harmless enough. One way to state it is: There is no preferred frame of reference for measuring motion. That is, there is no way to define absolute rest. Albert Einstein used this principle in his theory of special relativity (SR) in 1905. He added another: It is a property of space and time that the speed of light is the same for all observers, no matter how the light source moves. Of course he didn’t think of spaceships; he thought of trains. He explained what we see when we watch fast-moving meter sticks and clocks.

Ideas of time started to go seriously wrong two years later when German mathematician Hermann Minkowski (Einstein’s former teacher) invented spacetime. He advocated multiplying time t by the constant speed of light c to get a new variable ct, which has units of miles or kilometers like a space dimension. Instead of three space dimensions called x, y, z and one time dimension t, he proposed a space of four dimensions, x, y, z and ct. To emphasize how they may be seen as all the same they are often called x₁, x₂, x₃ and x₄. With this tweak, SR equations took on a neater form that seemed so beautiful (he said in 1908, in a famous speech) they must reveal a whole new truth about, not Einstein’s moving sticks and clocks, but space and time:

The concepts of space and time that I want to introduce to you are based on experimental physics. Therein lies their strength. Their import is radical. From now on, space alone and time alone should become mere shadows and only some kind of union of the two should maintain independence.

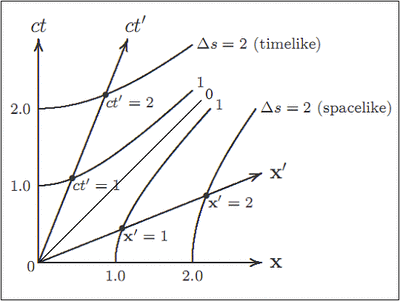Einstein saw Minkowski’s mash-up of space and time as a cute math trick. Minkowski promoted it as a new view of reality. He died from appendicitis before facing questions that this leap of faith implies. To this day a flood of physics follows Minkowski, sweeping his philosophical ‘reality’ along with it. For example (from eminent American physicist and educator, David Hestenes):

The standard model for spacetime is a real 4D Minkowski vector space M4called Minkowski spacetimeor (by suppressing the distinction between the model and the physical reality it is supposed to represent) simply spacetime.

This kind of physics is convenient. It says: There is no unmoving frame of reference; there is no absolute time; space and time are indistinct and intermingled. These philosophic facts are built into today’s physics and its math, as taught in universities.

But they’re not facts. Nor is this the only kind of physics that we have.

Next week: You can’t fool all the physicists all the time.

Sources:

Hermann Minkowski (1908), “Raum und Zeit”, Jahresberichte der Deutschen Mathematiker-Vereinigung, Leipzig: B. G. Teubner, 1909, http://de.wikisource.org/wiki/Raum_und_Zeit_%28Minkowski%29; passage quoted is my translation.

David Hestenes (2003), “Spacetime Physics with Geometric Algebra”, American Journal of Physics, vol. 71, p. 691; http://.geocalc.clas.asu.edu/pdf/SpacetimePhysics.pdf

Other Reading:

Dava Sobel (1995), Longitude, New York: Walker & Company; review Christopher Lehmann-Haupt (1997), “The Biggest Peril to Ships for Most of History”, The New York Times on the Web, http://www.nytimes.com/books/97/03/09/bsp/longitude.html

Daryl Janzen (2014), “Einstein’s Cosmological Considerations”, Ithaca: Cornell University Library, http://arxiv.org/pdf/1402.3212v1

Image Sources:

John Norton (2012), “Special Theory of Relativity: Adding Velocities”, Einstein for Everyone, http://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters/Special_relativity_adding/index.html

Burt Jordaan (2006), Relativity 4 Engineers, http://www.einsteins-theory-of-relativity-4engineers.com, Fig. 2.7; http://cr4.globalspec.com/blogentry/11156/The-Half-Twin-Puzzle

Special thanks to Canadian cosmologist Daryl Janzen for suggesting the topic and for helpful comments.