Science Seen Physicist and Time One author Colin Gillespie helps you understand your world.
A mysterious new shape seems to say something fundamental about the nature of the universe. Can we understand its message?
 Plato set out to explain everything with five perfect shapes. His theory died centuries ago. But in 2013 a shape called the amplituhedron burst upon the science scene. Physicists find it performs a miracle. But they don’t know how. The answer may hold a deep truth physics can sense but can’t quite find.
Plato set out to explain everything with five perfect shapes. His theory died centuries ago. But in 2013 a shape called the amplituhedron burst upon the science scene. Physicists find it performs a miracle. But they don’t know how. The answer may hold a deep truth physics can sense but can’t quite find.
Understanding the miracle and how it points to a deep truth begins with a task that is routine for physicists and obscure for everyone else—figuring the odds two subatomic particles will interact when they meet.
For example, quarks and gluons meet in atomic nuclei. A green quark can interact with a green-antiblue gluon and become a blue quark and vice versa. The Feynman diagram shows the simplest way this interaction can occur. Quantum theory provides a formula to calculate its probability of happening. This event may seem trivial but it is important: theory says these interactions hold nuclei together. Without them we would instantly explode.
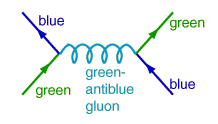 The trouble is there are many more complicated ways to yield the same result. For example that gluon can give rise to a virtual quark-antiquark pair that recombines to form a gluon (not shown). One must include all possible contributions if the calculation is to get the right answer. Even simple interactions could involve millions of complex terms. Serious calculations need supercomputers.
The trouble is there are many more complicated ways to yield the same result. For example that gluon can give rise to a virtual quark-antiquark pair that recombines to form a gluon (not shown). One must include all possible contributions if the calculation is to get the right answer. Even simple interactions could involve millions of complex terms. Serious calculations need supercomputers.
Many terms turn out to be infinite. Physicists devise a kludgy way to cancel them. In the end one can get an answer that turns out to be right. But getting there is an ugly, costly mess. That is, it was—until the amplituhedron hit the town.
Doggedly following a trail of sometimes loose associative clues, Iranian-American-Canadian physicist Nima Arkani-Hamed and his Czech student Jaroslav Trnka devised this new mathematical object. It lives in a topologic realm of symmetries. As is needed for a relational (or background-free) theory of quantum gravity, it abandons locality and does not use 3D space and time. It involves twistor space (with four complex vector dimensions). The “volume” of each amplituhedron is a relatively simple calculation. It turns out to be equal to the probability that particles will interact in space and time. Instead of ugly this theory is beautiful; but, as the authors say, it is ‘representing the physics without reference to standard physical ideas’.
The miracle is this gives the right answer for the probabilities. Now why would it be so?
Let’s follow a further trail that links two other topologically-minded thinkers who deal in symmetries, British physicist Sir Roger Penrose and Australian physicist Sundance Bilson Thompson. Penrose, whose seminal ideas on entropy were the subject of last week’s post, invented twistor theory in 1980 as a path to a theory of quantum gravity; but it did not seem to lead to practical results. And in 2008 Bilson-Thompson showed how the known subatomic particles correspond precisely to the topology of braided Planck-scale twists. In other words, he sees the constituents of matter and energy as purely relational.
It’s hard to know where to begin with background independence. As Italian physicist Carlo Rovelli said, ‘Everybody says they want background independence, and then when they see it they are scared to death by how strange it is.’
Could the amplituhedron be a back-door way of tapping into this strange world? Plato would be pleased.
Image credits:
Andy Gilmore, http://www.agilmore.com/Amplituhedron
R. Nave, http://hyperphysics.phy-astr.gsu.edu/hbase/Particles/expar.html

No comments yet.